튜링기계와 컴퓨터과학
[영혼을 위한 과학스프: 튜링기계와 컴퓨터과학]
본 기획은 세계를 인식하는 패러다임 변화에 큰 영향을 미친 핵심이론들을 하나씩 소개하면서, 각 이론에 직관적으로 접근할 수 있는 통로인 과학소설을 함께 추천한다. 일반대중의 접근이 지나치게 어렵다고 여겨지는 과학의 전문화/분과학문화에 문제제기하되, 과학이라는 진리를 인스턴트화하는 작업에도 반대한다. 이번 지면에는 앨런 튜링의 튜링기계 원리를 통해 컴퓨터과학의 시작을 이해해본다. <편집자 주>
무한하지 않지만 끝없이 유한한 기계

글을 쓰고 유용한 정보를 찾고, 또 일상의 휴식을 즐기는 게임에서조차 어느 하나 컴퓨터를 거치지 않은 것이 없다. 삶의 패러다임이 변했다고 말할 정도로 컴퓨터는 견고하고 세밀하게 우리 삶 속에 파고들었다. 그렇다면 일상의 패러다임을 바꾼 컴퓨터과학의 시작은 어디부터였을까. 그 첫발을 앨런 튜링의 ‘튜링기계(Turing machine)’를 통해 이야기하고자 한다. 앨런 튜링이 대중에게 다가온 건 지난 2월에 개봉한 영화 <이미테이션 게임>에서였다. 영화에서는 앨런 튜링이 ‘에니그마’라는 독일의 암호 기계를 해독하기 위해 튜링기계에 매달리는 장면이 나온다. 그는 튜링기계를 통해 알고리즘과 계산 개념을 형식화하여 큰 공헌을 하였으며, 또한 튜링 테스트를 고안해 인공지능 연구에도 큰 영향을 끼쳤다.
컴퓨터과학의 시초는 바로 ‘괴델의 불완전성 정리(Goedel’s incompleteness theo-rems)’에 대한 앨런 튜링의 증명에서 엿볼 수 있다. 1928년 수학자 다비트 힐베르트는 ‘원칙적으로 수학의 모든 문제를 순서대로 해결할 수 있는 일반적인 기계적 절차가 있는가’라는 문제를 제기했다. 이는 모든 수학을 풀 수 있는 알고리즘이 존재하는가에 대한 질문이며, 수학의 추론과정에서 기계적 패턴을 찾으면, 자동으로 수학의 모든 사실을 풀 수 있을 거라는 생각이었다. 하지만 1931년 쿠르트 괴델은 불완전성 정리를 통해 그것이 불가능함을 증명했다. 이 정리는 “기계적 방식만으론 수학의 모든 사실을 만들어 낼 수 없다”는 내용인데, 아무리 추론규칙들을 잘 만들어도, 기계적인 방식만으론 참인지 거짓인지 판단할 수 없는 명제가 항상 존재한다는 증명이었다. 당시 이는 학계에서 큰 충격이었고, 케임브리지 수학과를 졸업한 앨런 튜링도 불완전성 정리에 관심을 두게 된다.
1936년 앨런 튜링은 <계산 가능한 수와 결정문제의 응용에 관하여(On Computable Numbers, with an Application to the Entscheidungsproblem)>라는 논문에서 튜링기계라는 가상의 기계를 구현하여 기계적인 방식을 적용해 괴델의 정리를 증명한다. 튜링은 이 증명에서 간단한 기계부품들을 통해 하나의 특별한 기계를 만드는데 이것이 바로 ‘보편만능의 기계(Universal Machine)’였다.
튜링이 풀어가는 불완전성 정리
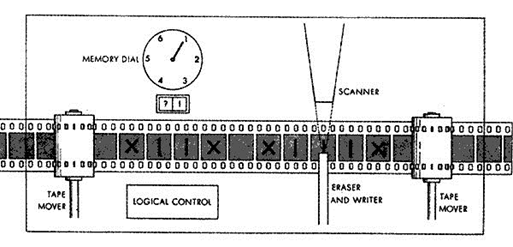
튜링기계는 다섯 종류의 기계부품으로 구성되어있다. 바로 ▲테이프 ▲테이프에 기록되는 기호 ▲테이프에 기록된 기호를 읽고 쓰는 장치 ▲장치의 상태들 ▲기계의 작동규칙표이다. 작동 방법으로는 어떤 기호들을 테이프에 넣고 쓰게 될 것인지, 어떤 기호들로 상태를 구분할지, 작동규칙표는 무엇인지, 테이프의 시작 형태와 기계의 시작상태 기호, 테이프 시작위치가 정해진다. 이렇게 정해진 기계는 작동규칙표에 정의된 규칙대로 작동하면서 정해진 계산을 한다. 튜링머신은 수학적 원리를 통해 만들어진 가상의 기계이지만, 오늘날의 컴퓨터에서 그 모습을 볼 수 있다. 테이프는 메모리칩으로, 테이프에 기록된 기호를 읽고 쓰는 장치는 메모리 입출력 장치로 구현되었고, 작동규칙표는 중앙처리장치(CPU)로 발전했다. 따라서 해당 기계에 실행하고자 하는 일을 메모리에 표현해 소프트웨어로 만들어 입력하면 컴퓨터는 정의대로 일을 수행한다.
다시 튜링기계로 돌아와, 튜링은 그의 논문에서 기계적이라는 것이 무엇인지 정의하기 위해 위의 다섯 가지 부품들을 정의하고, 이것을 통한 증명을 기계적인 방식이라고 정의한다. 그리고 이를 위해 튜링기계의 ‘궁극의 기계’인 보편만능의 기계를 생각해낸다. 이 기계에서 주목할 점은 첫째, 기계에 정해진 테이프와 기호만으로도 임의의 튜링기계(작동규칙표와 테이프, 현재 기계 상태 기호)를 만들 수 있다는 점이다. 이를 통해 임의의 다른 기계의 정의 또한 입력 받을 수 있다. 둘째로는, 테이프에 표현되어있는 기계의 정의에 따라 그 동작을 따라할 수 있는 작동규칙표를 정의한 것이다. 이러한 방식을 통해 튜링기계는 하나지만 모든 튜링기계를 흉내 낼 수 있으며, 자신이 설정한 범주의 모든 기계적인 계산을 하나의 기계(보편만능의 기계)로 돌려볼 수 있게 된다.
튜링기계는 상상할 수 있는 유한한 계산은 가능하지만, 모든 계산을 할 수 있지는 않다. 튜링기계 테이프에는 고유의 자연수 하나만 표현할 수 있기에 튜링기계의 수는 ‘셀 수 있을 만큼 많은 수’이다. 같은 무한이라 할지라도 자연수보다 실수가 더 크기에 튜링기계는 모두 참인 명제를 만들어 낼 수가 없다. 이것이 튜링기계의 한계점으로, ‘멈춤 문제(halting problem)’와 연결된다. 멈춤 문제란 임의의 프로그램과 그 프로그램에 대한 임의의 값을 입력하고 실행할 때 이 프로그램이 계산을 끝내고 멈출지, 아니면 무한하게 계속 계산을 할지 결정하는 걸 말한다. 앨런 튜링은 튜링기계가 자연수라는 것과, 보편만능의 기계와 ‘대각선 논법(diagonalization)’을 통해 멈춤 문제를 푸는 튜링기계가 존재할 수 없음을 밝히며, 모두 참인 사실을 만들 수 있는 기계는 존재하지 않음을 증명해 간다.
이처럼 튜링은 불완전성 정리를 가상의 튜링기계라는 기계적인 방법을 통해 증명해냈다. 그리고 튜링기계라는 상상의 기계는 이제 컴퓨터라는 사물로 실현되었다. 수학적 사고체계와 기계를 결합한 컴퓨터를 통해 인간의 삶으로 침투한 튜링기계는, 한 세기를 바꿀 만큼 큰 변화의 도구로 자리 잡았다. 튜링의 보편만능의 기계는 이제 또 다른 혁명의 가능성을 기다리고 있다.
글: 황나리 편집위원 / 감수: 임동근
※참고: 컴퓨터과학이 여는 세계 / 이광근 저
